Herramientas matemáticas para la localización espacial.

Descripciones espaciales y transformacionales                

Un robot es un manipulador lo que implica que se desplazaran piezas y herramientas en el espacio mediante mecanismos. Esto conduce a la necesidad de representar posiciones y orientaciones de todo el conjunto que forma el manipulador. Es necesario definir sistemas de coordenadas y desarrollar convenciones para la representación de los movimientos del manipulador.

El termino descripción se utiliza en robótica para describir un sistema de manipulación como las piezas, herramientas y el mismo manipulador con respecto a la descripción de posiciones, orientaciones y de una entidad que contiene ambas descripciones denominada Trama.

Describiendo una posición

Al establecer un sistema de coordenada podemos ubicar cualquier punto en el universo con un vector de posición de orden 3 x 1. En la descripción de un sistema manipulador es común definir muchos sistemas de coordenadas, además del sistema de coordenadas universal, estos deben etiquetarse con información que identifique en cuál de estos sistemas están definidos.

Ejemplo

Este vector tiene valores numéricos  que indican distancias sobre los ejes del vector universal

Figura1: Posición indicada por el vector A_P (posición) sobre el vector universal.

Se puede también describir la posición de un punto en el espacio a través de las representaciones de coordenadas esféricas o cilíndricas.

Describiendo una orientación

No solo es necesario definir la posición del objeto a manipular, sino que también es necesario conocer la orientación del cuerpo manipulador con respecto a nuestro marco de referencia universal, el punto representado en la Figura2 está en la punta de los dedos del manipulador, pero no se conoce la orientación de este, el brazo podría cambiar la orientación de cada una de las articulaciones y aun podría mantenerse en la posición del espacio del punto de interés, entonces para conocer la orientación del manipulador se le adjunta un sistema de coordenadas que denominaremos {B} y luego se describe este sistema de coordenadas relativo al sistema de referencia {A}.

Figura2: Se observa la posición y orientación del manipulador.

El manipulador posee su propia dirección de coordenadas {B} el cual debe escribirse en función del sistema de coordenadas {A} quedando      donde {A} representada en la parte superior izquierda el vector de referencia universal y {B} representa el vector referenciado con respecto al vector universal {A} En teoría este arreglo de representación de vectores se le denomina matriz de rotación representada de esta forma

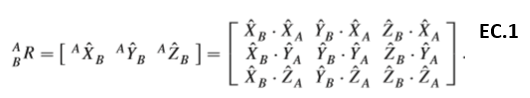
Cada columna de la matriz tiene las coordenadas de un eje del marco seguidor (ejes del Manipulador) con respecto al marco de referencia universal. Por ejemplo, la primera columna contiene las coordenadas del eje X del manipulador representada en el arreglo de ejes del marco de referencia universal. Similarmente la segunda y la tercera columna poseen las coordenadas del eje Y y Z del manipulador representadas con respecto al vector universal. Siempre que se represente la posición de un punto con un vector la orientación de este se hará por medio de una matriz de rotación.

Es importante el conocimiento de las propiedades de álgebra lineal para entender las trasformaciones que pueden adoptar las matrices, se sabe que el producto punto de dos vectores unitarios es el coseno del Angulo entre ellos entonces las matrices de rotación pueden llamarse cosenos de dirección.

                                                                                                                                     Se puede expresar esta misma matriz como la descripción del Vector de la trama de {A} relativa a {B} mediante la transpuesta de la misma matriz.

O esta misma matriz puede adoptar igualdades respecto a la                                                             matriz {A} relativa a {B}.

 

Descripción de una trama   

Para describir en un instante de tiempo donde se sitúa la mano del manipulador es necesario conocer la posición y orientación estas dos variables en conjunto se les denomina en robótica como trama esta está compuesta por cuatro vectores de tres elementos, uno proporciona la información de la posición y los otros tres de la orientación que a su vez se puede definir como una matriz rotacional. Por lo tanto, la trama {B} se describe definiendo los vectores de este con  respecto a {A} quedando una matriz rotacional y  como un vector de posicion que describe el origen de la                        trama {B}    

 

Figura3: Trama de un punto con posición y orientación con respecto al vector universal {A}

Las tramas también pueden estar en un conjunto de las cuales es necesario saber cómo ubicar esa información cabe mencionar que se posee de un vector universal del cual se pueden extender un conjunto de “ramificaciones” de posiciones y orientaciones si se decide analizar una de las tramas es necesario conocer su origen y como está representada con respecto a la trama de origen. Para proceder se debe generalizar la idea de que una trama es una descripción de un sistema de coordenadas relativo a otro donde este cuenta con orientación y posición. Si analizamos la Trama {C} se observa que esta depende de la orientación y posición de {R} el cual esta referenciada al vector universal {O}, un ejemplo clásico es un robot con marco de referencia de la tierra, ósea que se puede tomar la idea que esta es la forma habitual de representación universal.

Figura4: Ramificaciones de tramas

 

Ya que conocemos los conceptos básicos que caracterizan una trama conjunta con su posición y orientación es necesario también conocer los cálculos involucrados para poder cambiar las descripciones de una trama a otra.

Tramas Trasladadas

Este problema se presentaría por ejemplo cuando el robot se desplazará sin cambiar la orientación solo tendríamos un problema de distancia (Posición). Entonces la trama {B} con respecto a {A} solo difiere por su traslación en el espacio de trabajo donde es la variable a considerar.

Si analizamos la trama {B} de la Figura5 estas poseen la misma orientación y para poder calcular la descripción del punto de interés con respecto a la trama de referencia universal {A} se hace una suma de vectores donde 

Figura5: Trama trasladada

Trama Rotada

Para el análisis de la trama rotada es necesario conocer las propiedades de las matrices y hacer un esfuerzo de entender las diferentes formas de representar una matriz. Partiendo de esta idea se sabe que para representar la orientación es necesario una matriz de rotación 3 x 3 que involucran dos vectores donde {B} es representado sobre el vector universal {A}.

De la siguiente matriz rotacional se puede notar que las columnas son los vectores unitarios de {B} escritos en {A} y que las filas son los vectores unitarios de {A} pero escritos en {B} de esta forma se puede escribir la matriz de rotación de dos formas diferentes como un conjunto de tres vectores columnas o como un conjunto de tres vectores filas.

Figura6: Se muestra las dos formas de representación de la matriz de rotación.

Ahora lo que realmente deseamos conocer es la relación del punto de interés P con respecto al vector de referencia universal y este cálculo es posible ya que conocemos la descripción de la orientación de {B} con respecto a {A} ya que se tienen una matriz de rotación, pero cabe destacar que esta tiene componentes rotados los cuales se desean representar en función del punto de interés A (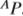) entonces se procede a escribir los vectores unitarios de {B} en función de {A} Quedando la proyección como el producto punto de los vectores.

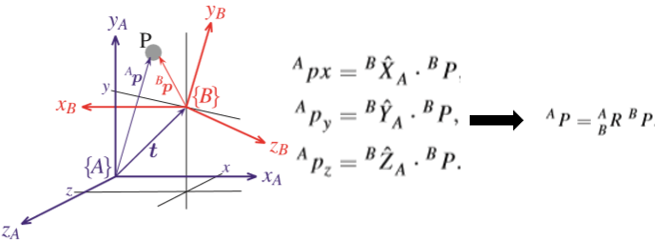
Figura7: Trama {B} rotada y descripción matemática del punto P de interés.

Ejemplo de una trama rotada

El siguiente ejercicio muestra una trama {B} rotada θ=30º con respecto a la trama universal {A} sobre el vector Z. donde Z apunta hacia fuera de la pantalla. Encontrar A_P

R/. Para proceder se sabe que la orientación de la trama {B} esta alterada y por lo tanto la orientación se debe escribir en función de la trama universal {A}. Ya que el ejercicio solo nos indica que solo el eje Z afecta la orientación con θ=30º desorientados.

Por la ecuación 3 de los cosenos de dirección podemos definir que la matriz de rotación afecta solo al rotacional RotZ (Z, θ)

Por lo tanto, la matriz de rotación de {B} con respecto al vector universal {A} queda definida:

 Así el punto de interés con respecto a la orientación y posición de la trama {B} Con respecto a la trama universal {A}  queda definido por las anteriores coordenadas.

Para aclarar un poco mas que paso aquí, imaginémonos que tenemos que dar con una dirección de una calle la cual nos urge dar con ella se nos ha orientado que con respecto al edificio del “Cine” es 2 cuadras al sur; pero con respecto al “Hotel” queda a 1 cuadras al este y casi 2 cuadras al sur para llegar al mismo punto.

“Cine” =                             “Hotel” =

Quedando entonces definido el mismo punto en el espacio el cual se puede  ver desde dos tramas diferentes.